 |
|
Theory
The propagation properties of electromagnetic waves in (unmagnetized) plasma are largely determined by the relation of their frequency to the (electron) plasma frequency,
![]() ,
,
where e and m are the electron charge and mass, respectively, n is their number density, and ε0 is the vacuum permittivity. Interactions between two waves are based on modulations of the electron mass and/or the electron density. Both are due to the forced oscillation in the electromagnetic fields: while the former follow from the relativistic mass dependence on the oscillation velocity, the latter are a consequence of the ponderomotive potential, which is equal to the oscillation energy.
Raman Amplification
Raman scattering occurs when the frequencies of two waves differ by approximately the plasma frequency, so that longitudinal oscillations at that frequency are resonantly excited, which then scatter one wave into the other, and vice versa. Either a scattered wave can grow spontaneously from noise, or a seed pulse can be amplified at the expense of a strong pump. It is this latter case that interests us. Under the right circumstances, the seed pulse is compressed during amplification, leading to a very short and intense pulse. See here for more details.
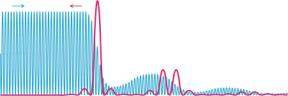
Electromagnetically Induced Guiding
A different process may take place when the frequency of the longitudinal modulations is far from the plasma resonance. Under certain conditions, the scattering of two waves into each other has a focusing effect counteracting the vacuum diffraction.

Electromagnetically Induced Transparency
A wave with frequency below the plasma frequency, cannot propagate through the plasma on its own, but interaction with a second wave allows propagation. Calculations predict transparency, when the difference or sum of the laser frequencies is just below the plasma frequency.

Wakefield Interactions and Electron Acceleration
After an electromagnetic pulse has passed through plasma, the remaining density inhomogeneities lead to a wakefield, which oscillates at the plasma frequency. Its phase velocity coincides with the group velocity of the pulse. There are different possibilities how a second pulse can interact with this field: If the wake is weak, i.e. the corresponding density perturbations are small, a wave scattered at it will undergo a frequency shift of . The more interesting case is that of a strong wake; a wave propagating in the opposite direction may then be reflected at it, leadin to a large Doppler shift due to the high velocity of the wake. On the other hand, a pulse propagating with the wake and shorter than its wavelength may be compressed in it due to the longitudinal dependence of the density.
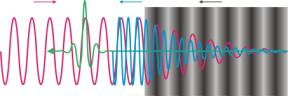
top Wakefields may also be used to trap and accelerate electrons. Ideally, these should reach the group velocity of the laser pulse which generated the wake, close to the vacuum speed of light. See the ALPHA-X Project for more details.

Laser-Undulator Radiation
Also under investigation in the ALPHA-X
Project is the topic of radiation generation in the periodic magnetic
field of an undulator filled with plasma. The ponderomotive force due
to a short intense laser pulse sets the plasma electrons in longitudinal
motion. The magnetic field then accelerates them in a transverse direction,
so that they can radiate along the undulator axis. The spatial periodicity
of the magnetic field together with the propagation of the laser pulse
leads to a matching condition for the phases of the radiation generated
at different times, which may be satisfied for frequencies either in the
far infrared or in the X-ray spectrum.
Interesting questions related to this scheme concern the
influence of a finite amplitude of the magnetic field on the propagation
of the laser pulse – at high amplitudes, the periodically magnetized
plasma represents an optical lattice, with consequently allowed and forbidden
frequency bands.
|
Part of the
Scottish Universities
Physics Alliance (SUPA) and the
Department
of Physics, |
